La parola della settimana: ASINTOTO

asìntoto 

(Incroci obbligati 91143)

Sost. s. m. (dal gr. ἀσύμπτωτος [asýmptotos] "che non s'incontra", comp. di ἀ- priv. e dell'agg. verbale di συμπίπτω "incontrarsi"): [mat.] retta a cui una curva si avvicina indefinitamente senza mai raggiungere il contatto; tangente all’infinito.

In matematica, in particolare nel calcolo e nell'algebra, il concetto di asintoto è fondamentale. Esso consente di comprendere più a fondo il comportamento di funzioni e curve geometriche, soprattutto quando queste si estendono verso l'infinito.

Un asintoto è essenzialmente una linea a cui una curva si avvicina senza mai raggiungerla. Questo comportamento si verifica indipendentemente dalla distanza percorsa dalla curva.

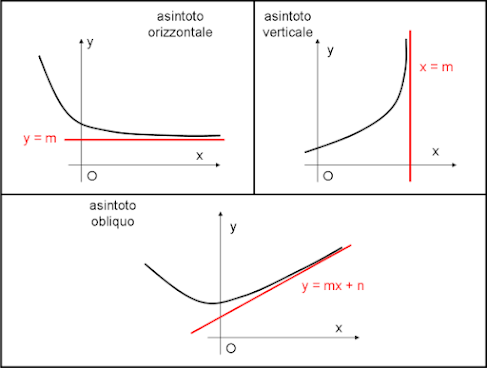
Gli asintoti possono essere verticali, orizzontali o obliqui.

Asintoto verticale: Si verifica quando il valore y = f(x) tende all'infinito (positivo o negativo) man mano che la x si avvicina a un certo valore. L'asintoto verticale si incontra spesso nelle funzioni razionali in cui il denominatore può essere zero.

Asintoto orizzontale: Descrive il comportamento di una curva y = f(x) quando il valore di x si dirige verso l'infinito (positivo o negativo). In questo caso, i valori della y si avvicinano a un valore costante. Sono comuni nelle funzioni in cui il grado del numeratore è inferiore o uguale al grado del denominatore.

Asintoto obliquo: Si verifica quando la curva si avvicina a una linea che non è né orizzontale né verticale. Questo accade di solito quando il grado del numeratore è pari al grado del denominatore più uno.

Immagine tratta da: www.infinitoteatrodelcosmo.it

Gli asintoti sono fondamentali nel campo del calcolo numerico per comprendere i limiti e la continuità. Aiutano a tracciare i grafici delle funzioni e ad analizzare il loro comportamento ai valori estremi. In ingegneria e fisica, gli asintoti sono utilizzati per modellare scenari reali in cui i valori si avvicinano ma non raggiungono mai una certa soglia.

Il concetto di asintoto è quindi una finestra sul comportamento delle funzioni quando si estendono all'infinito. La comprensione degli asintoti permette ai matematici di cogliere le sfumature del comportamento delle funzioni. Sia in ambito teorico che nelle applicazioni pratiche, la conoscenza degli asintoti riveste notevole importanza.